Κβαντικές Θεωρίες Πεδίου σε ισχυρή σύζευξη υπό το πρίσμα της ολογραφίας και της ολοκληρωσιμότητας

Τομέας Πυρηνικής Φυσικής και Στοιχειωδών Σωματιδίων, Τμήμα Φυσικής, ΕΚΠΑ

Μέλη ερευνητικής ομάδας

Καθηγητής Κωνσταντίνος Σφέτσος
Μεταδιδάκτορες: Γεώργιος Γεωργίου, Δημήτριος Ζωάκος και Κωνσταντίνος Σιάμπος
Διδάκτορες: Παντελής Πανόπουλος και Ευτυχία Σαγκριώτη
Υποψήφιος Διδάκτορας: Γεώργιος Παππάς

Χρηματοδοτήσεις

1. 1^η Προκύρυξη ερευνητικών έργων ΕΛ.ΙΔ.Ε.Κ. για την ενίσχυση των μελών ΔΕΠ και Ερευνητών/τριών και την Προμήθεια Ερευνητικού Εξοπλισμού Μεγάλης Αξίας (Κύριος ερευνητής: Κ. Σφέτσος).
2. 1^η Προκύρυξη ΕΛ.ΙΔ.Ε.Κ. για την ενίσχυση μεταδιδακτόρων (Κύριος ερευνητής: Γ. Γεωργίου).
3. Διδακτορικοί υπότροφοι ΙΚΥ: (Ε. Σαγκριώτη, Γ. Παππάς)

Η πλήρης κατανόηση φυσικών διεργασιών σε ισχυρά συζευγμένα συστήματα, αποτελεί θεμελιακής φύσης ερώτημα τόσο στη φυσική υψηλών ενεργειών όσο και στη φυσική συμπυκνωμένης ύλης.

Συγκεκριμένα παραδείγματα αποτελούν το φαινόμενο του εγκλωβισμού σε θεωρίες βαθμίδας όπως η κβαντική χρωμοδυναμική (ΚΧΔ) και η συμπεριφορά ψυχρών Φερμιονικών ατόμων, που δεν επιδέχονται αντιμετώπιση μέσω συμβατικών διαταρακτικών μεθόδων. Ένας από τους τρόπους μελέτης ισχυρά συζευγμένων, σχετικιστικών και μη συστημάτων, είναι με τη χρήση της ολογραφικής αρχής [1] (βλέπε Σχήμα 1). Μέσω αυτής, ισχυρά συζευγμένα συστήματα απεικονίζονται σε ασθενώς συζευγμένες θεωρίες βαρύτητας μιας επιπλέον χωρικής διάστασης, οι οποίες μπορούν να μελετηθούν με χρήση διαταρακτικών μεθόδων. Το πρωταρχικό και πλέον μελετημένο παράδειγμα της ολογραφικής αντιστοιχίας είναι η δυïκή αντιστοίχιση της μέγιστα υπερσυμμετρικής και σύμμορφης θεωρίας βαθμίδας σε μια θεωρία χορδών στον καμπύλο χωροχρόνο γεωμετρίας AdS₅ Χ S⁵ [2]. Επιπλέον χαρακτηριστικό αυτού του παραδείγματος είναι ότι είναι  ολοκληρώσιμο δηλαδή πλήρως επιλύσιμο.

Στο παραπάνω γενικό πλαίσιο η δραστηριότητα της ομάδας μας επικεντρώνεται στη διατύπωση και μελέτη γενικεύσεων της αντιστοιχίας στις οποίες απουσιάζει πλήρως η υπερσυμμετρία, η σύμμορφη συμμετρία ή/και η ολοκληρωσιμότητα. Τέτοιες γενικεύσεις προσομοιάζουν ποιοτικά την ΚΧΔ καθώς και συστήματα συμπυκνωμένης ύλης.

Μια πολύ ενδιαφέρουσα γενίκευση της αντιστοιχίας είναι η φωτοειδής διπολική παραμόρφωση, η οποία περιγράφει ισχυρά συζευγμένα συστήματα πολλών σωματιδίων με μη-σχετικιστική συμμετρία Schrödinger σε τρείς χωροχρονικές διαστάσεις [3]. Η παραμόρφωση περιγράφει μη-τοπικού χαρακτήρα αλληλεπιδράσεις κατά μήκος της φωτοειδούς διάστασης ενώ έχει μη-σχετικιστική σύμμορφη συμμετρία κατά μήκος των υπολοίπων. Η δυϊκή περιγραφή αυτού του φυσικού συστήματος δίνεται από μια θεωρία βαρύτητας σε χωροχρόνο με συμμετρία Schrödinger.

Η παραπάνω φωτοειδής παραμόρφωση μπορεί να μελετηθεί με τη χρήση εκτεταμένων «γιγαντιαίων» βαρυτονίων. Η ενέργεια αυτών των εκτεταμένων λύσεων, παρουσία της παραμόρφωσης, είναι μικρότερη από την ενέργεια των αντίστοιχων σημειακών λύσεων (βλέπε Σχήμα 2). Αυτή η συμπεριφορά είναι ασυνήθης, καθώς τόσο στον αρχικό χωροχρόνο γεωμετρίας AdS₅ Χ S⁵ όσο και σε άλλες παραμορφώσεις αυτού, η εκτεταμένη λύση έχει ενέργεια μεγαλύτερη από αυτή της σημειακής [4].

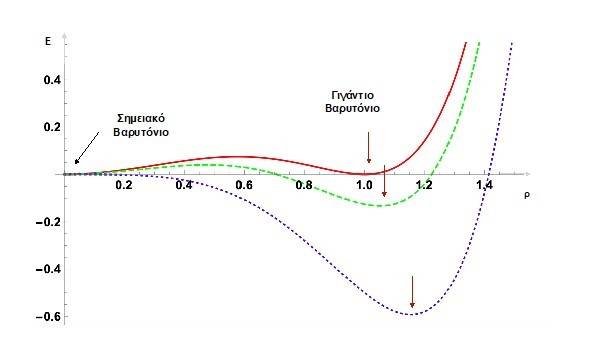
Θεωρίες που προκύπτουν από παραμορφώσεις σύμμορφων θεωριών πεδίου (ΣΘΠ) μπορούν να περιγράψουν τη συμπεριφορά συστημάτων πολλών σωματιδίων γύρω από το κρίσιμο σημείο, στη φυσική συμπυκνωμένης ύλης. Μια τέτοια κατηγορία είναι οι λ-παραμορφώσεις, οι οποίες γενικά είναι ολοκληρώσιμες και μη-σύμμορφες. Αυτά τα πρότυπα παρεμβάλλονται μεταξύ μιας ΣΘΠ για μεγάλες ενέργειες (υπεριώδες) και μιας ισχυρά συζευγμένης θεωρίας πεδίου για μικρές ενέργειες (υπέρυθρο) ή εναλλακτικά δυο ΣΘΠ σε υπεριώδες και υπέρυθρο αντίστοιχα [5].

Η κβαντική μελέτη των προαναφερθέντων προτύπων οδήγησε στον υπολογισμό συναρτήσεων συσχέτισης πρωτευόντων τελεστών μέσω των οποίων εξαγάγαμε την ακριβή εξάρτηση της παραμέτρου παραμόρφωσης λ καθώς και τις ανώμαλες διαστάσεις των παραπάνω τελεστών από την ενεργειακή κλίμακα [6]. Τα αποτελέσματά μας ισχύουν για κάθε τιμή της ενέργειας ακόμα και πέραν του διαταρακτικού ορίου κάτι σπάνιο σε κβαντικές θεωρίες πεδίου. Επιπρόσθετα βρήκαμε τη ακριβή εξάρτηση του πλήθους των βαθμών ελευθερίας αυτών των προτύπων από την ενεργειακή κλίμακα [7], το οποίο είναι μοναδικό στη διεθνή βιβλιογραφία. Τα παραπάνω υποδείγματα βρίσκουν εφαρμογές, π.χ. σε μη-Φερμιονικά ρευστά (non-Fermi liquids) στα οποία υπάρχουν ισχυρές κβαντικές διακυμάνσεις κοντά στην ενέργεια Fermi [8].

Συνεχίζουμε την προσπάθεια μας στην μελέτη κβαντικών θεωριών πεδίου σε ισχυρή σύζευξη με την βοήθεια της ολογραφικής αρχής αλλά και της ολοκληρωσιμότητας για την ενδελεχή μελέτη φυσικών συστημάτων παρουσία συνόρων και ατελειών.

Ενδεικτική βιβλιογραφία

[1] G. ‘t Hooft, Conf.Proc.C 930308 (1993), 284-296.
     L. Susskind, J. Math. Phys. 36 (1995), 6377-6396.

[2] J. M. Maldacena, Adv. Theor. Math. Phys. 2 (1998), 231-252.

[3] D. T. Son, Phys. Rev. D78 (2008), 046003.

[4] G. Georgiou and D. Zoakos, JHEP 03 (2020), 185.
      G. Georgiou, K. Sfetsos and D. Zoakos, JHEP 08 (2019), 093.

[5] K. Sfetsos, Nucl. Phys. B880 (2014), 225-246.
     G. Georgiou and K. Sfetsos, JHEP 11 (2017), 078.

[6] G. Georgiou, K. Sfetsos and K. Siampos, Nucl. Phys. B909 (2016), 360-393.

[7] G. Georgiou, P. Panopoulos, E. Sagkrioti, K. Sfetsos and K. Siampos, Phys. Lett.B782 (2018), 613-618.
     G. Georgiou, G. Pappas and K. Sfetsos, Nucl. Phys. B958 (2020), 115138.

[8] N. Andrei, M. R. Douglas and A. Jerez, Phys. Rev. B58 (1998), 7619-7625.