Ο καθηγητής Ιωάννης Κ. Δημητρίου δημοσίευσε μια μελέτη στο έγκριτο περιοδικό Optimization Methods & Software με τίτλο “Least Squares Monotonic Unimodal Approximations to Successively Updated Data and an Application to a Covid-19 Outbreak”. Η μελέτη αναπτύσσει έναν αλγόριθμο προσέγγισης δεδομένων εν εξελίξει, αλλοιωμένων από σφάλματα, ώστε να εκτιμήσει το σημείο στροφής (ακρότατο) μιας έξαρσης (outbreak). Η μελέτη έχει αποφύγει τη χρήση παραμέτρων ή υποθέσεις πιθανοτήτων που συνήθως εφαρμόζεται σε πολλές άλλες τεχνικές προσεγγίσεων. Για την ακρίβεια, έχει αναπτυχθεί ένας αλγόριθμος που υπολογίζει αυτόματα άριστες, μονότονα αύξουσες και φθίνουσες προσεγγίσεις ελάχιστων τετραγώνων, οι οποίες επιτρέπουν την εξαγωγή της κρίσιμης τάσης καθώς το σύνολο των δεδομένων εξελίσσεται. Ο αλγόριθμος αντιμετωπίζει αποτελεσματικά τις μη κανονικότητες που παρατηρούνται στα δεδομένα, με άριστη υπολογιστική απόδοση πολυπλοκότητας O(n) για ανάλυση σε πραγματικό χρόνο, όπου n είναι το τρέχον πλήθος δεδομένων. Θεμελιώνεται με επιχειρήματα βελτιστοποίησης και δημιουργεί ένα αξιόπιστο πλαίσιο εκτίμησης για την ανάλυση δεδομένων από μονοκόρυφες εξάρσεις. Η μελέτη περιέχει επίσης μια τεκμηριωμένη εφαρμογή του αλγόριθμου σε δεδομένα Covid-19 και επιπροσθέτως προτείνει μια επιτυχή βελτίωση υφιστάμενων διαδικασιών με υβριδικό συνδυασμό του αλγόριθμου. Συγκεκριμένα, προετοιμάζει (initialize) τον υπολογισμό της μη γραμμικής βελτιστοποίησης του επιδημιολογικού μοντέλου Richards, και τα αριθμητικά αποτελέσματα επιβεβαιώνουν ορισμένα πλεονεκτήματα σε σχέση με τη συνήθη χρήση αυτού του μοντέλου που απαιτεί ρύθμιση παραμέτρων και παρεμβάσεις του αναλυτή. Η μεθοδολογία που προτείνεται έχει εφαρμογές πέραν της επιδημιολογίας, σε κάθε τύπο εξάρσεων, συμπεριλαμβανομένων κοινωνικών, οικονομικών, συμπεριφορικών και φυσικών φαινομένων, παρέχοντας εκτιμήσεις για το επερχόμενο ακρότατο σημείο. Αυτό το χαρακτηριστικό είναι κρίσιμο για την κατανόηση μονοκόρυφα εξελισσόμενων δεδομένων, αλλά και χρήσιμο για τη λήψη αποτελεσματικών αποφάσεων στην πράξη. Στο Σχήμα 1 επιδεικνύονται ορισμένες διαμορφώσεις της άριστης προσέγγισης και η εκτίμηση του ακρότατου, καθώς εισέρχονται τα δεδομένα στον υπολογισμό. Η μέθοδος μπορεί να υποστηρίξει τους υπεύθυνους χάραξης πολιτικής σε προκλήσεις δημόσιας υγείας, αποκαλύπτοντας την εξέλιξη της δυναμικής των επιδημιών και επιτρέποντας τεκμηριωμένες αντιδράσεις. Αναλόγως, και για άλλους τομείς που παρουσιάζονται εξάρσεις.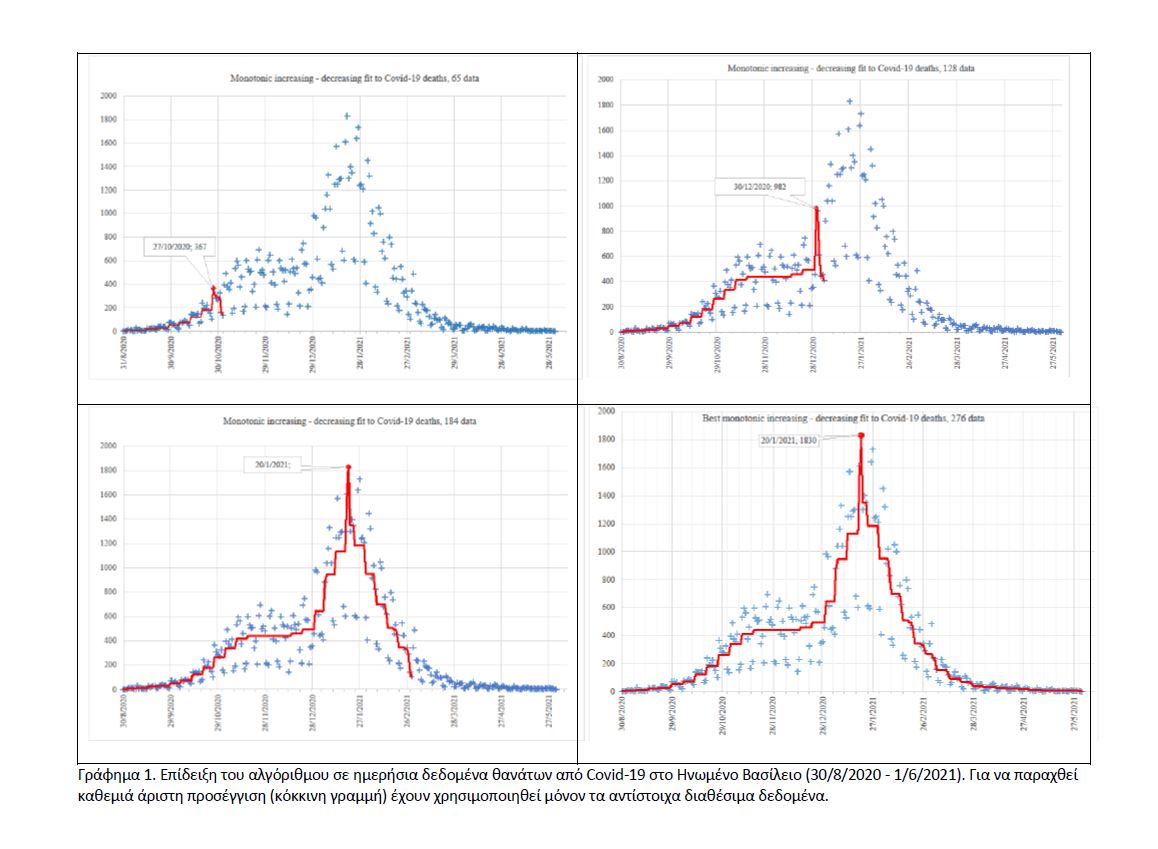 
Ο Δημητρίου δήλωσε: «Στο μέτρο των γνώσεών μας, δεν έχει προηγηθεί παρόμοια διερεύνηση. Αξιοποιώντας αυτή τη μέθοδο, στοχεύουμε στη βελτίωση της προβλεψιμότητας του απόγειου των εξάρσεων και την παροχή μιας σαφέστερης κατανόησης της εξέλιξής τους. Τα ευρήματα θα μπορούσαν να αποδειχθούν χρήσιμα για τη διαμόρφωση των αντιδράσεων όχι μόνο απέναντι σε πανδημίες, αλλά και σε άλλα πολύπλοκα συστήματα. Με μοναδική υπόθεση από την πλευρά του αναλυτή ότι επέρχεται ένα outbreak, είναι αξιοσημείωτο ότι η μέθοδος εκτιμά αυτόματα το ακρότατο από τα ίδια τα δεδομένα στον βέλτιστο χρόνο.» Το πλήρες άρθρο είναι διαθέσιμο στη διεύθυνση https://doi.org/10.1080/10556788.2024.2428475 Η περίληψη δίνεται εδώ.
Για περαιτέρω ερωτήσεις ή περισσότερες πληροφορίες, παρακαλούμε επικοινωνήστε με τον κ. Δημητρίου στη διεύθυνση email που παρέχεται παραπάνω. Αναφορές: Demetriou, I.C. “Least Squares Monotonic Unimodal Approximations to Successively Updated Data and an Application to a Covid-19 Outbreak”, Optimization Methods & Software, Volume 39, 2024 – Issue 6, pp. 1464-1494, DOI: 10.1080/10556788.2024.2428475.
