Χρήστος Αθανασιάδης, Καθηγητής, Τμήμα Μαθηματικών, ΣΘΕ, ΕΚΠΑ
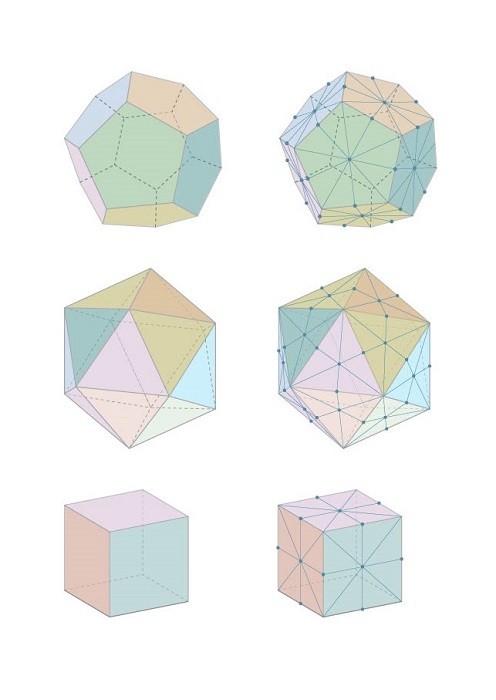
Ένα θεμελιώδες πρόβλημα της γεωμετρικής συνδυαστικής είναι να χαρακτηρίσει κανείς, ή έστω να συλλέξει μη τετριμμένες πληροφορίες, για τα διανύσματα (λίστες αριθμών) που προκύπτουν απαριθμώντας γεωμετρικούς σχηματισμούς διαφόρων διαστάσεων που ορίζονται από απλά, διακριτά γεωμετρικά αντικείμενα. Για παράδειγμα, τα γεωμετρικά αντικείμενα μπορεί να είναι πεπερασμένοι σχηματισμοί σημείων στην ευθεία, στο επίπεδο, στον τρισδιάστατο χώρο ή, γενικότερα, σε έναν Ευκλείδειο χώρο τυχαίας διάστασης και οι γεωμετρικοί σχηματισμοί να είναι τα σημεία, οι ευθείες, τα δισδιάστατα επίπεδα, και ούτω καθεξής, που ορίζονται από τα δοσμένα σημεία, ή μπορεί τα γεωμετρικά αντικείμενα να είναι κυρτά πολύγωνα, τρισδιάστατα πολύεδρα όπως ο κύβος, το δωδεκάεδρο και το εικοσάεδρο (βλέπε Σχήμα 1, αριστερά) ή, γενικότερα, πολύεδρα τυχαίας διάστασης ή τριγωνισμοί αυτών και οι γεωμετρικοί σχηματισμοί να είναι οι όψεις τους (κορυφές, ακμές, δισδιάστατες όψεις, και ούτω καθεξής) δοσμένης διάστασης.
Αν και είναι σχετικά στοιχειώδη και εύκολο να διατυπωθούν, τα προβλήματα αυτά είναι αρκετά δύσκολα, ιδιαίτερα στις υψηλές διαστάσεις. Έχουν απασχολήσει τους μαθηματικούς για αιώνες και η επιτυχής αντιμετώπισή τους συχνά απαιτεί εργαλεία και συνδυασμούς μεθόδων από διάφορες περιοχές των σύγχρονων θεωρητικών μαθηματικών. Την τελευταία δεκαετία έχει επιτευχθεί εντυπωσιακή πρόοδος η οποία, μεταξύ άλλων, περιλαμβάνει: (α) τον πλήρη χαρακτηρισμό των f-διανυσμάτων των τριγωνισμών μιας σφαίρας τυχαίας διάστασης (απόδειξη της g-εικασίας για σφαίρες) από τον Karim Adiprasito και από τους Σταύρο Παπαδάκη και Βασιλική Πετρωτού (ερευνητές από το Τμήμα Μαθηματικών του Πανεπιστημίου Ιωαννίνων) [1,3,10] και (β) τη λογαριθμική κοιλότητα των συντελεστών του χαρακτηριστικού πολυωνύμου (απόδειξη της εικασίας των Heron-Rota-Welsh) [2] και του πολυωνύμου της ανεξαρτησίας (απόδειξη της εικασίας του Mason) [8] ενός τυχαίου μητροειδούς και την απόδειξη των ανισοτήτων Dowling-Wilson για τους αριθμούς Whitney ενός τυχαίου γεωμετρικού συνδέσμου [9] από τον June Huh και συνεργάτες του, αποτελέσματα για τα οποία πολύ πρόσφατα (Ιούλιος 2022) ο τελευταίος τιμήθηκε με το μετάλλιο Fields στα μαθηματικά.
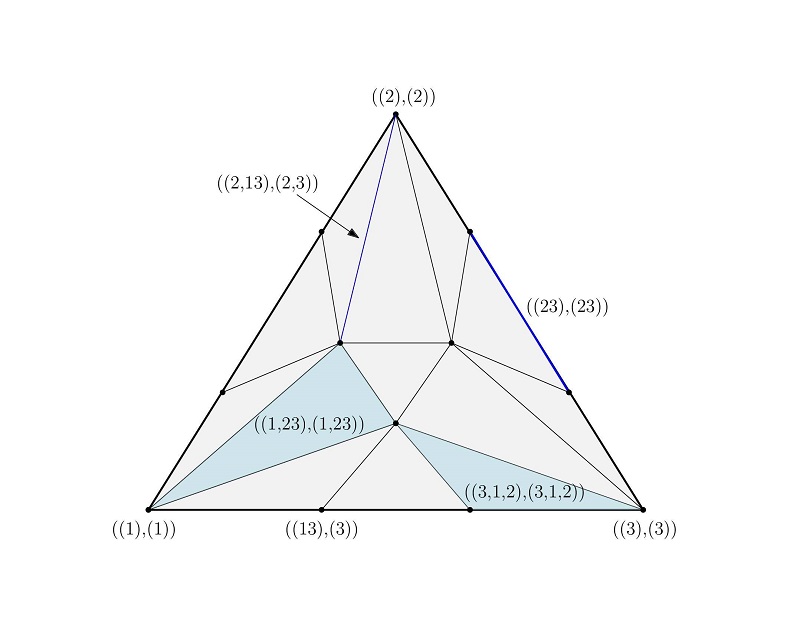
Μια από τις ισχυρότερες και λεπτότερες επιθυμητές ιδιότητες για τα διανύσματα των αριθμών που συζητάμε είναι ότι το πολυώνυμο με συντελεστές τους αριθμούς αυτούς έχει μόνο πραγματικές ρίζες. Είναι ανοιχτό πρόβλημα (στο οποίο δεν είχε επιτευχθεί σημαντική πρόοδος την τελευταία δεκαπενταετία) να αποφασισθεί αν το διάνυσμα που προκύπτει απαριθμώντας τις όψεις της βαρυκεντρικής υποδιαίρεσης ενός πολυέδρου (βλέπε Σχήμα 1, δεξιά) τυχαίας διάστασης έχει πάντοτε αυτή την ιδιότητα (είναι γνωστό ότι το ερώτημα έχει θετική απάντηση για simplicial πολύεδρα, δηλαδή πολύεδρα οι γνήσιες όψεις των οποίων είναι ευθύγραμμα τμήματα, τρίγωνα, τετράεδρα, και ούτω καθεξής, όπως το εικοσάεδρο). Σε έρευνα χρηματοδοτούμενη από το ΕΛ.ΙΔ.Ε.Κ (2η Προκήρυξη Ερευνητικών Έργων για την ενίσχυση Μελών ΔΕΠ και Ερευνητών/τριών) με Επιστημονικό Υπεύθυνο τον υπογράφοντα, δίνεται θετική απάντηση στο ερώτημα για πολύεδρα τυχαίας διάστασης των οποίων οι γνήσιες όψεις είναι κύβοι [4], καθώς και για κάποιες οικογένειες πολυέδρων τυχαίας διάστασης που δεν ανήκουν στις ειδικές κατηγορίες των simplicial ή των κυβικών πολυέδρων [7]. Επιπλέον, το πρόβλημα μελετάται και για τριγωνισμούς γενικότερους από τις βαρυκεντρικές υποδιαιρέσεις με ενδιαφέρουσες συνδυαστικές ιδιότητες [5,6,7], όπως είναι οι αντιπρισματικοί τριγωνισμοί (βλέπε Σχήμα 2, παρμένο από το άρθρο [5]).
[1] K. Adiprasito, Combinatorial Lefschetz theorems beyond positivity, arXiv:1812. 10454.
[2] K. Adiprasito, J. Huh and E. Katz, Hodge theory for combinatorial geometries, Ann. Math. 188 (2018), 381-452.
[3] K. Adiprasito, S.A. Papadakis and V. Petrotou, Anisotropy, biased pairing and the Lefschetz property for pseudomanifolds and cycles, arXiv:2101.07245.
[4] C.A. Athanasiadis, Face numbers of barycentric subdivisions of cubical complexes, Israel J. Math. 246 (2021), 423-439.
[5] C.A. Athanasiadis, J-M. Brunink and M. Juhnke-Kubitzke, Combinatorics of antiprism triangulations, Discrete Comput. Geom. 68 (2022), 72-106.
[6] C.A. Athanasiadis and E. Tzanaki, Symmetric decompositions, triangulations and real-rootedness, Mathematika 67 (2021), 840-859.
[7] C.A. Athanasiadis and K. Kalampogia-Evangelinou, Chain enumeration, partition lattices and polynomials with only real roots, arXiv:2205.03796.
[8] J. Huh, B. Schroter and B. Wang, Corelation bounds for fields and matroids, J. European Math. Soc. 24 (2022), 1335-1351.
[9] J. Huh and B. Wang, Enumeration of point, lines, planes, etc., Acta Math. 218 (2017), 297-317.
[10] S.A. Papadakis and V. Petrotou, The characteristic 2 anisotropicity of simplicial spheres, arXiv:2012.09815.